Confirmation and the Generalized Nagel-Schaffner Model of Reduction: A Bayesian Analysis
Abstract
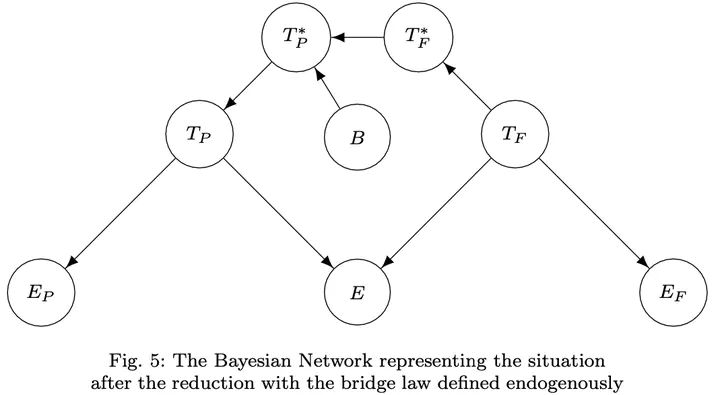
In their 2010 paper, Dizadji-Bahmani, Frigg, and Hartmann (henceforth ‘DFH’) argue that the generalized version of the Nagel-Schaffner model that they have developed (henceforth ’the GNS’) is the right one for intertheoretic reduction, i.e. the kind of reduction that involves theories with largely overlapping domains of application. Drawing on the GNS, DFH (2011) presented a Bayesian analysis of the confirmatory relation between the reducing theory and the reduced theory and argued that, post-reduction, evidence confirming the reducing theory also confirms the reduced theory and evidence confirming the reduced theory also confirms the reducing theory, which meets the expectations one has about theories with largely overlapping domains. In this paper, I argue that the Bayesian analysis presented by DFH (2011) faces difficulties. In particular, I argue that the conditional probabilities that DFH introduce to model the bridge law entail consequences that run against the GNS. However, I also argue that, given slight modifications of the analysis that are in agreement with the GNS, one is able to account for these difficulties and, moreover, one is able to more rigorously analyse the confirmatory relation between the reducing and the reduced theory.